L'économie des réseaux sociaux : quelques réflexions sur ses méthodes et ses résultats

Christophe Bravard est Professeur des Universités en sciences économiques depuis 2012. Il travaille actuellement à l'Université Grenoble Alpes et effectue ses recherches au sein de l'unité mixte de recherche GAEL (Laboratoire d'Économie Appliquée de Grenoble). Il est spécialiste d'économie des réseaux, d'économie mathématique et de théorie des jeux. Ses recherches ont été publiées dans les revues Economic Theory, International Journal of Industrial Organization ou encore le Journal of Mathematical Economics. Il a présenté ses travaux aux étudiants de l'École Normale Supérieure de Lyon le 13 octobre 2017, lors de la première séance du Séminaire "Actualité de la recherche en économie" organisé par Laurent Simula, professeur d'économie à l'ENS de Lyon.

Interview de Christophe Bravard, chercheur en économie des réseaux sociaux

Cette interview a été réalisée par Raphaël Chekroun, étudiant en Informatique Fondamentale à l'École Normale Supérieure de Lyon, ayant choisi une mineure en économie dans le cadre de son diplôme. Ayant apprécié l'utilisation d'un cadre très formel et mathématique pour répondre à des questions importantes dans le domaine des sciences sociales, il a choisi d'interroger Christophe Bravard sur son parcours, ses motivations, les outils qu'il mobilise et son positionnement général au sein de l'économie.

L'économie mathématique est généralement définie comme l'utilisation de méthodes mathématiques pour représenter des théories économiques ou analyser des problèmes économiques. Cette définition me semble un peu large dans la mesure où elle ne permet pas de faire de distinction entre l'économie théorique et l'économie mathématique. De mon point de vue, l'originalité de l'économie mathématique est d'utiliser des méthodes que l'on trouve essentiellement en mathématique ; l'économie mathématique ne se réduit pas à l'utilisation ou à l'introduction d'objets empruntés aux mathématiques en économie. Pour illustrer mon propos, je prendrai deux exemples.

1. L'une des forces de la théorie mathématique est de montrer que des objets, a priori très différents, sont en réalité de même nature ; par exemple les nombres entiers et les polynômes sont de «même nature» du fait de certaines de leurs caractéristiques. Évidemment, les mathématiciens ont dû construire toute une théorie permettant de réunir ces deux objets dans un même cadre. L'économie mathématique procède de la même façon. Par exemple, la théorie des jeux vise à construire des cadres à l'intérieur desquels des situations, a priori très différentes, seront regroupées car elles ont les mêmes propriétés. Nous pouvons illustrer notre propos à travers deux situations :

a. Un duopole de Bertrand différencié, c'est-à-dire une situation où deux firmes entrent en concurrence en prix et produisent des produits similaires bien que différents (Renault vend des Kangoo et Citroën des Berlingo) ;

b. La production de miel par un apiculteur et la production de fruit par un propriétaire de verger. Cette situation est caractérisée par le fait que la quantité de fruits obtenue par le propriétaire du verger croît avec la quantité de ruches mises en place par l'apiculteur (et donc avec la quantité de miel produite). Symétriquement la quantité de miel obtenue croît avec la quantité d'arbres plantés (et donc la quantité de fruits produite).

Ces deux situations semblent, de prime abord, très dissemblables. Pourtant, la théorie des jeux va les réunir dans une même classe. En effet, lorsque nous analysons ces deux situations du point de vue des agents économiques, des traits communs surgissent. D'abord, les agents économiques devront effectuer des choix : la fixation d'un prix, d'une quantité de ruches ou d'arbres fruitiers. Ensuite, le profit d'un agent économique dépendra de ses propres choix, mais également des choix réalisés par l'autre agent. Enfin, les choix optimaux des agents seront une fonction croissante des choix de l'autre agent. Dans le cas du duopole de Bertrand, si l'agent A augmente son prix, alors l'agent B a intérêt à augmenter son prix. Dans le cas de l'apiculteur et du propriétaire de verger, si l'apiculteur augmente sa quantité de ruches, alors le propriétaire a intérêt à augmenter sa quantité d'arbres fruitiers. Du fait de ces similarités, ces deux situations vont appartenir à la même classe de jeu. En étudiant cette classe de jeu à un niveau suffisamment général, il est possible de donner les mécanismes principaux à l'œuvre dans ces situations sans avoir à étudier chacune d'entre elles.

2. Une autre caractéristique de la théorie mathématique est de présenter des axiomatisations. Autrement dit, partir «d'hypothèses» considérées comme données et en déduire des résultats [1]. L'axiomatisation est utilisée de manière importante en théorie des jeux coopératifs [2]. L'un des buts de la théorie des jeux coopératifs consiste à donner les conditions (axiomes) permettant d'obtenir un partage «juste» d'une valeur créée entre plusieurs agents. Plus précisément, l'objectif est de définir des conditions permettant d'obtenir, pour tout type de problème de partage, l'existence et l'unicité du partage juste. L'originalité de cette démarche est d'offrir une clarté absolue quant aux conditions sous lesquelles un partage sera considéré comme juste. En outre, elle permet, dans une certaine mesure, d'éviter certains débats peu scientifiques liés à la sensibilité de l'objet d'étude.

Non, je n'ai pas les compétences qui me permettraient de créer une théorie mathématique. Mon objectif consiste à utiliser des résultats ou des modes de raisonnement mathématique pour rendre compte de situations pertinentes du point de vue de l'économie théorique.

Un spécialiste de l'histoire des idées économiques serait sans doute plus pertinent pour répondre à ce type de question. Pour autant, il me semble que la spécificité de la science économique en tant que science sociale est d'avoir très tôt adopté un langage mathématique (au XIXème siècle). Cette possibilité a été permise par la création du concept d'homo œconomicus, c'est-à-dire de l'objet «agent maximisateur», et de l'existence du calcul différentiel. Au cours de la deuxième partie du XXème siècle, de nouvelles théories et de nouveaux outils conceptuels ont été créés. Ils ont permis des avancées significatives en termes de compréhension de certains mécanismes fondamentaux en économie industrielle, en économie internationale... Du fait de l'apparition de ces outils, une partie importante de la communauté des économistes s'est spécialisée dans des domaines théoriques où le formalisme était relativement important, au cours des années 1980 et 90. Ceci explique sans doute la réaction des étudiants des ENS et de l'Université Paris-Dauphine en 2000. Depuis, nous assistons, en sciences économiques, à un déplacement important de la communauté vers des domaines appliqués et expérimentaux. Il me semble donc que la critique formulée en 2000 envers la discipline a beaucoup moins de sens aujourd'hui.

La microéconomie a, dès son origine, emprunté des raisonnements aux sciences de la nature en particulier à la mécanique. Une nouvelle fois un historien de la pensée économique serait beaucoup plus compétent que moi, mais il me semble que Léon Walras, l'un des pères fondateurs du raisonnement microéconomique, s'est largement inspiré de la mécanique dans ses travaux. En outre, au cours de son histoire, la théorie économique a toujours emprunté des outils aux sciences exactes et a employé de nombreuses analogies avec des théories issues de ces dernières.

Concernant le fait que les sciences économiques pourraient tenir une position à l'interface entre sciences sociales et sciences exactes/expérimentales, je ne pense pas que l'économie joue ce rôle. Je crois que la science économique joue un rôle particulier en sciences sociales du fait (i) des hypothèses qu'elle pose sur le comportement des agents : les agents sont considérés en tant qu'agents maximisateurs ou stratèges, et (ii) des méthodes qu'elle emploie, par exemple l'économétrie. L'une des différences majeures de mon point de vue entre les sciences dures et les sciences sociales concerne le fait que toutes les sciences sociales visent à rendre compte des mêmes phénomènes : les comportements des agents. Ainsi un économiste peut étudier les comportements criminels, les comportements électoraux, etc., de même un sociologue ou un psychologue peuvent étudier des comportements économiques, par exemple les comportements d'achats. De ce fait, les sciences sociales se distinguent entre elles par les méthodes qu'elles emploient ; chacune dispose de ses spécificités méthodologiques, mais aucune d'entre elles ne peut, évidemment, épuiser son objet.

Mes travaux proviennent de recherches empiriques concernant les réseaux sociaux. Ces recherches ont montré que la qualité du réseau social auquel appartient un agent est un déterminant important de sa réussite sociale, par exemple en termes de capacité à trouver un emploi (voir ci-dessous). Une littérature en théorie économique est apparue qui vise à la fois à expliquer l'architecture des réseaux par des comportements maximisateurs de la part des agents, et à expliquer le comportement des agents du fait de l'influence de leurs pairs. Les deux problématiques centrales dans mes travaux sont d'une part, dans quelle mesure l'existence de réseaux sociaux conduit les agents à se coordonner sur des états efficaces socialement (ou non) et d'autre part, dans quelle mesure l'existence de réseaux sociaux peut renforcer (ou non) les inégalités entre les agents. L'objectif central étant de proposer des politiques publiques permettant de réduire les inégalités en agissant sur les réseaux sociaux des agents économiques (généralement de façon indirecte).

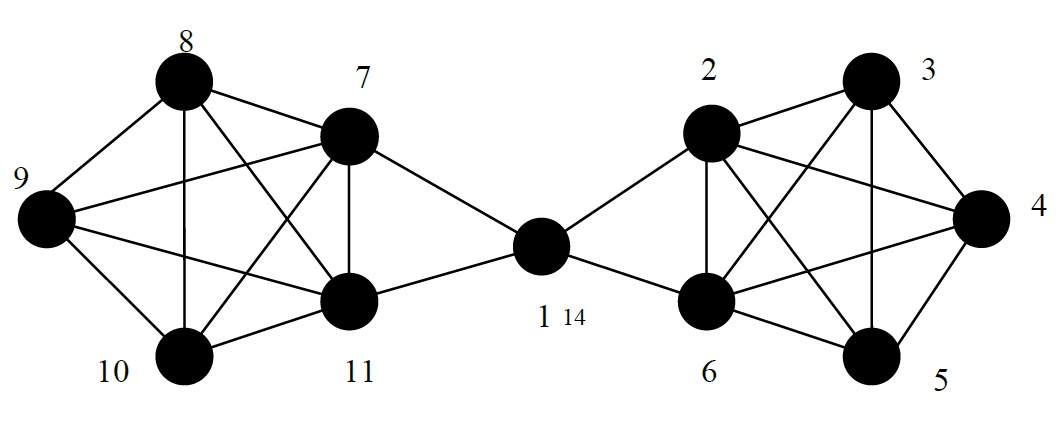
Les outils d'analyse sont (i) la théorie des graphes où nous identifions les agents avec les nœuds et leurs relations avec les arêtes, (ii) la théorie des jeux qui permet de caractériser le comportement maximisateur des agents économiques. Ces outils nous permettent de caractériser des équilibres que nous pouvons comparer à des états efficaces d'un point de vue social. Ils nous permettent également d'examiner les conséquences de la mise en place de certaines politiques publiques sur les équilibres.

Propos recueillis par Raphaël Chekroun.

Réseaux sociaux et participation au marché du travail

Dans un travail pionnier en théorie des réseaux, Mark Granovetter (1973) a réalisé une étude empirique sur des habitants d'une ville du Massachusetts. Dans cette étude, plus de 50% des emplois des agents ont été obtenus par le truchement de leur réseau social. Antoni Calvo-Armengo et Matthew O. Jackson (2004) ont complété ce travail en supposant que le réseau social des agents permet l'obtention d'informations concernant les opportunités d'emplois ; ils étudient les conséquences du réseau social sur la dynamique d'emploi des agents. Plus précisément, les auteurs souhaitent rendre compte du fait stylisé suivant : la participation au marché du travail d'un agent est très différente en fonction de son appartenance à certains groupes sociaux ou ethniques. Par exemple, D. Card and A.B. Krueger (1992) observent une non-participation au marché du travail 2,5 à 3 fois plus élevée pour les personnes noires que pour les personnes blanches.

Dans leur modèle, A. Calvo-Armengo et M.O. Jackson supposent que les agents perdent avec une certaine probabilité leur emploi à chaque période, et qu'avec une certaine (autre) probabilité, les agents participant au marché du travail obtiennent de l'information concernant la disponibilité d'emplois. Ainsi, un agent qui n'a pas perdu son emploi et obtient une information sur des emplois vacants peut transmettre cette information aux membres de son réseau social. En conséquence, plus le réseau social d'un agent est de qualité au regard de l'employabilité de ses membres, plus il y a de chance que cet agent obtienne de l'information quant à la disponibilité d'un emploi. Le modèle de Calvo-Armengo et Jackson induit qu'il devrait y avoir, empiriquement, une corrélation entre les niveaux de chômage des agents appartenant aux mêmes réseaux sociaux. Cette corrélation a effectivement été trouvée dans plusieurs études empiriques (G. Topa, 2001 ; T.G. Conley et G. Topa, 2001).

Notons que cette corrélation positive a des conséquences quant à la participation ou non au marché du travail de la part des agents. À titre d'illustration, considérons deux réseaux identiques, excepté le fait que dans l'un d'eux, disons le réseau 1, les agents disposent d'une employabilité supérieure aux agents appartenant à l'autre (le réseau 2). Du fait des différences initiales d'employabilité, les agents du réseau 2 ont plus de chance de ne plus participer au marché du travail (et donc ne participent plus activement au réseau). Cette non-participation a des conséquences sur tous les membres du réseau social des agents qui ne participent plus au marché du travail. En effet, chaque chômeur réduit la possibilité d'obtenir de l'information sur un emploi vacant de l'ensemble de ses voisins (présence d'une externalité négative des chômeurs). Ainsi, il apparaît une sorte de multiplicateur social de non-participation au marché du travail, mais aussi des effets de contagion. En outre, la dynamique d'emploi conduit à des différences importantes concernant la durée de chômage des agents. Plus généralement, du fait des effets multiplicateurs et de la contagion, des conditions initiales proches en termes d'employabilité, peuvent conduire à des résultats très différents en termes d'insertion professionnelle et de durée de chômage des individus.

Ce modèle permet de mettre en avant de nouveaux mécanismes justifiant l'intervention des autorités publiques. Chaque dépense réalisée pour l'aide à l'emploi aura non seulement des effets directs sur les agents visés, mais également des effets indirects sur les membres de leur réseau social.

Christophe Bravard (février 2018).

Références :

Granovetter, M.S. (1973), "The strength of weak ties", American Journal of Sociology, vol.78 (6), p.1360-1380. Trad. franç. dans : Mark Granovetter, Le Marché autrement. Les réseaux dans l'économie, Desclée de Brouwer, 2000.

Calvó-Armengol A., Jackson M.O. (2004), "The Effects of Social Networks on Employment and Inequality", American Economic Review, Vol.94 (3), p.426-454.

Card D., Krueger A.B. (1992), "School Quality and Black-White Relative Earnings: A Direct Assessment", Quarterly Journal of Economics, vol.107 (1), p.151-200.

Topa G. (2001), "Social Interactions, Local Spillovers and Unemployment", Review of Economic Studies, vol.68 (2), p.261–95.

Conley T.G., Topa G. (2001), "Socio-Economic Distance and Spatial Patterns in Unemployment", Mimeo, New York University.

Pour aller plus loin

Télécharger le support de présentation de Christophe Bravard lors du séminaire "Actualité de la recherche en économie" à l'ENS de Lyon (octobre 2017).

Olivier Barbié, "Qu'est-ce que l'économie des réseaux ?", Œconomia, vol.1, n°1, 2011, p.119-127.

En anglais :

Matthew O. Jackson, "Networks in the Understanding of Economic Behaviors", Journal of Economic Perspectives, vol.28 (4), 2014, p.3-22.

Matthew O. Jackson, Brian W. Rogers, Yves Zenou, "Networks: An Economic Perspective", August 2016.

Notes

[1] En mathématiques, parmi les axiomatiques les plus connues, citons celles d'Euclide ou de Peano.

[2] Plusieurs «prix Nobel» d'économie se sont intéressés à ce type de problématique, citons J. Nash, R. Myerson, L. Shapley.